Les lambroquins à La Réunion :

géométrie du quotidien, géométrie de l’infini

Dominique Tournès

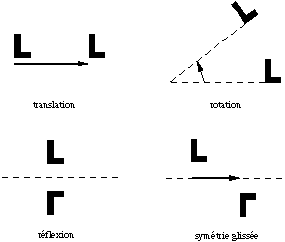
Maison à Cilaos

Dans l’île de La Réunion, chacun est familier des lambrequins, ces garnitures de bois ajourées qui décorent les varangues créoles. Localement, on les appelle aussi "lambroquins" (orthographe qui reçoit notre préférence et que nous utiliserons dans la suite) ou encore, de manière imagée et savoureuse, "dentelle la case". À l’origine, en Europe, les lambrequins étaient des bandes d’étoffe utilisées pour la décoration d’un casque, d’une cuirasse, d’une galerie de fen tre ou d’un ciel de lit. Ce furent ensuite des ornements découpés, en bois ou en métal, bordant un auvent. Sur les navires, les lambroquins bordaient le toit qui protège le nid de poule, lieu où le timonier tient la roue du gouvernail (cet endroit était aussi désigné par le mot marin "varangue"). Tout naturellement, c’est par la mer que les lambroquins sont arrivés à La Réunion : les charpentiers de marine qui construisirent les premières maisons de l’île ont adapté aux varangues des cases créoles la décoration des varangues des navires. Depuis, ces dentelles de bois sont devenues un élément significatif de l’architecture réunionnaise. Outre leur fonction décorative, elles remplissent une fonction utilitaire : en piégeant les eaux de ruissellement s’écoulant du toit et en les faisant dégoutter verticalement en avant de la façade, elles protègent cette dernière de l’humidité.

Deux ouvrages d’importance ont, jusqu’ici, été consacrés aux lambroquins de La Réunion : une passionnante brochure de Jean-Paul Egon (Les Lambroquins à La Réunion, CRDP de La Réunion, 1985) et un inventaire technique des motifs utilisés (Lambrequins, sous la direction de Tony Manglou, Commissariat à l’Artisanat, Conseil général de La Réunion, 1985). Dans les deux cas, l’étude, conduite du point de vue de l’architecte ou de l’artisan, est centrée sur les aspects fonctionnel, décoratif, artistique et symbolique des lambroquins. Aucun des deux ouvrages ne prend en compte le fait que ces dentelles de bois, en tant que dessins à motifs répétitifs, appartiennent d’abord à la géométrie. Il restait donc à décrire la structure mathématique sous-jacente à ces objets familiers de notre environnement quotidien. C’est ce que nous nous proposons de faire ici. Nous tenterons d’ tre accessible à tous en évitant tout formalisme spécialisé. Nous limiterons notre commentaire au minimum indispensable, laissant chacun bâtir sa propre théorie par la contemplation des figures et des photographies.

L’ornementation, sous son aspect premier, consiste en la répétition de formes. Dans la plupart des situations courantes, une forme élémentaire, appelée "motif", est reproduite à l’aide de symétries, de manière à engendrer un "dessin à motifs répétitifs" (qu’on peut appeler aussi "réseau"). Par le terme générique de "symétrie", nous désignons ici toute transformation qui conserve la forme et les dimensions du motif de base. Les décorateurs ayant surtout travaillé sur des réseaux à une ou deux dimensions, nous ferons donc, dans ce qui suit, de la géométrie plane. Les principales symétries planes sont bien connues de tous dans la mesure où elles sont étudiées pendant la dernière année de l’école élémentaire : ce sont les translations (déplacements d’une distance donnée dans une direction donnée), les rotations (d’un angle donné autour d’un centre donné) et les réflexions (appelées aussi symétries orthogonales par rapport à une droite). Aux trois types précédents, il faut ajouter les symétries glissées, obtenues en faisant suivre une réflexion par une translation parallèle à l’axe de la réflexion.

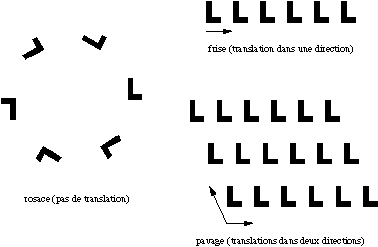
fig. 1. Les quatre types de symétries planes

On peut classer les dessins à motifs répétitifs à partir du nombre de directions selon lesquelles le dessin est invariant par translation. Si le dessin n’est conservé par aucune translation, on parle de "rosace". On trouve, par exemple, des rosaces parmi les vitraux des cathédrales. Plus près de nous, les jours de Cilaos sont aussi des rosaces. Seconde catégorie : un dessin invariant par translation dans une seule direction est appelé une "frise".

C’est le cas des galons, des pochoirs, des frises décorant certains monuments antiques comme le Parthénon… ou encore des lambroquins. Enfin, un dessin invariant par translation dans deux directions est appelé un "pavage". Le carrelage d’une pièce, le dessin d’un papier peint mural sont des exemples familiers de pavages. On peut remarquer que, dans l’ornementation, une rosace est une figure finie, tandis que les frises et les pavages sont, par essence, des figures infinies (m me si, concrètement, on ne peut en représenter qu’une partie). En quelque sorte, les frises et les pavages permettent d’introduire une image de l’infini au sein de la vie quotidienne.

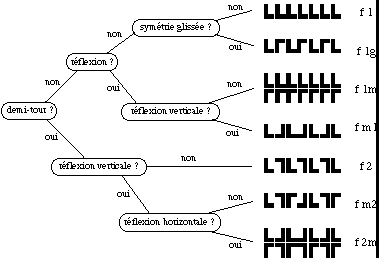
fig. 2. Les trois sortes de dessins à motifs répétitifs

Bien entendu, la conception d’un motif de base est totalement libre et offre au créateur une infinité de possibilités. Par contre, le nombre de façons d’engendrer un réseau à partir d’un motif de base est limité par des contraintes très fortes résultant de la structure mathématique de l’ensemble des symétries du plan. À la fin du dix-neuvième siècle, grâce à la théorie des groupes issue des travaux de Galois et Abel, les géomètres ont démontré qu’il n’existait que sept types possibles de frises et dix-sept types possibles de pavages. Il est intéressant de noter que tous les types théoriques de réseaux plans décrits par les savants avaient été découverts beaucoup plus tôt, de façon empirique, par les artisans. On trouve déjà tous les pavages possibles dans l’ornementation égyptienne, ou encore dans l’art islamique : c’est ainsi que des carrelages des dix-sept types peuvent tre contemplés à l’Alhambra de Grenade, lieu mythique que tout mathématicien se doit de visiter au moins une fois dans sa vie.

Mais revenons aux lambroquins, qui sont des frises. Les sept types de frises sont présentés sur la figure 3, accompagnés d’un algorithme permettant de déterminer à quel type appartient une frise donnée. La codification utilisée est celle des cristallographes : f signifie frise, m vient du mot anglais "mirror" (miroir, ou réflexion) et g vient de la locution anglaise "glide reflection" (symétrie glissée) ; le nombre 1 ou 2 représente l’ordre maximum d’une rotation conservant la frise (1 lorsqu’il n’y a pas de rotation, 2 lorsqu’il y a une rotation d’ordre 2, c’est-à-dire un demi-tour). Lorsque la lettre m ou g est placée après le nombre, il s’agit d’une réflexion ou d’une symétrie glissée par rapport à l’axe de la frise (axe "horizontal") ; lorsque la lettre m est placée avant le nombre, il s’agit d’une réflexion par rapport à un axe perpendiculaire à celui de la frise (axe "vertical"). Le codage fournit, en fin de compte, une liste minimale de symétries permettant, à partir du motif de base, d’engendrer le dessin qui sera ensuite reproduit à l’infini par translation.

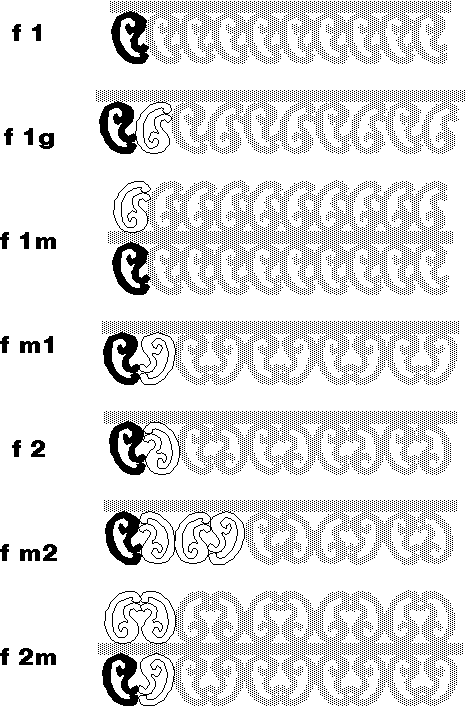
fig. 3. Algorithme de classification des frises

Théoriquement, on devrait pouvoir rencontrer sept types géométriques de lambroquins. Nous avons construit, sur la figure 4, ces sept types à partir d’un motif de base simplifié mais conforme à l’esprit des motifs réellement utilisés dans l’architecture créole.

fig. 4. Les sept types théoriques de lambroquins

Trouve-t-on réellement ces sept types à La Réunion ? Pour le savoir, nous avons mené une enqu te statistique dans les hauts de l’Ouest de l’île. Nous avons étudié cent exemples de lambroquins, et nous avons compté le nombre d’occurrences de chaque type. Voilà les résultats obtenus :

Le type le plus courant est incontestablement f m1, celui dont le dessin présente seulement une réflexion d’axe vertical. Les dessins des lambroquins f m1 sont extr mement variés, allant du plus simple au plus ouvragé (figure 5).

fig. 5. Un lambroquin de type f m1 au motif particulièrement ouvragé

Nous reviendrons longuement, à la fin de notre article, sur les caractéristiques de ce type prédominant. Pour l’instant, présentons brièvement les autres types rencontrés, ceux que l’on peut considérer comme exceptionnels dans l’architecture créole. Le cas des lambroquins f 1 est un peu à part. En effet, si nous avons trouvé deux cas qui relèvent vraiment de ce type (la figure 6 représente l’un d’eux), nous avons également rencontré huit exemplaires d’un m me dessin assez curieux (figure 7). À première vue, ce dessin a toutes les apparences d’un f m1 mais une observation plus attentive permet de découvrir une légère rupture de symétrie qui fait qu’il s’agit bien, en réalité, d’un f 1. Nous qualifierons cet exemple de "faux f m1". Il ne nous semble pas significatif dans la mesure où nous l’avons rencontré huit fois dans un périmètre assez restreint, alors qu’il n’est mentionné dans aucun des ouvrages que nous avons consultés. On peut penser que, sans doute, à un moment donné, un artisan des hauts de l’Ouest a fabriqué ce motif en série et l’a distribué dans son voisinage immédiat, sans influence notable sur le reste de la production réunionnaise.

fig. 6. Un lambroquin de type f 1

fig. 7. Un "faux f m1" qui est en réalité un f 1

Par ailleurs, il ne faut pas s’étonner si les types présentant une invariance par réflexion horizontale ou par demi-tour sont assez rares. En effet, m me si cela n’est en rien obligatoire, il semble naturel de les découper en deux bandes se répartissant de part et d’autre de la tranche du toit. Dans ces conditions, la partie haute n’a plus de fonction utilitaire liée à l’écoulement des eaux de pluie : sa présence, purement gratuite, remplit seulement une fonction esthétique. Les photographies suivantes fournissent un joli exemple de f 2m (figure 8) et l’unique exemple de f 2 que nous ayons trouvé (figure 9). Le type f 2 n’étant présent dans aucun des livres sur l’architecture réunionnaise, notre exemple est probablement, à ce jour, l’unique lambroquin de type f 2 répertorié à La Réunion.

fig. 8. Un lambroquin de type f 2m

fig. 9. L’unique exemple connu du type f 2

Les inventaires de Jean-Paul Egon et de Tony Manglou confirment largement nos observations. Jean-Paul Egon donne vingt exemples de motifs présentés comme représentatifs de l’architecture réunionnaise : tous, sans exception, sont du type f m1. La collection du Commissariat à l’Artisanat se veut plus exhaustive : on y trouve 157 exemples de lambroquins, dont 154 du type f m1, deux du type f 2m et un seul du type f m2. On peut donc considérer que, en dehors de quelques cas peu significatifs sans doute liés à des commandes de clients originaux, les artisans réunionnais ont toujours produit des lambroquins de type f m1, sans chercher à exploiter davantage les possibilités offertes par la géométrie.

Comment expliquer ce manque apparent d’imagination ? Pourquoi se limiter à une réflexion d’axe vertical alors qu’il y a d’autres symétries disponibles ? La réflexion d’axe vertical, ou symétrie bilatérale, joue un rôle particulier dans le monde vivant : c’est la symétrie du corps humain et de la plupart des organismes évolués. Or, l’architecture doit tre vue, avant tout, comme une élaboration symbolique transposant les caractéristiques fondamentales de la nature et, en premier lieu, celles de l’homme. En ce sens, il était inévitable que la symétrie bilatérale y occupe une place prépondérante. Si les carreleurs arabes ont pu, à l’Alhambra, réaliser les dix-sept sortes possibles de pavages, on pense que c’est à cause d’une donnée essentielle de la civilisation musulmane : l’interdiction de la représentation de la figure humaine et, plus généralement, des tres vivants. Soumis à cette forte contrainte, les artistes arabes se sont réfugiés dans l’ornementation géométrique abstraite. Peu à peu, ils en ont découvert empiriquement toutes les potentialités, trouvant par là le seul moyen d’exercer leur imagination. Pour les fabricants de lambroquins, la situation a toujours été différente. La case créole est un lieu intime, harmonieusement inséré dans une végétation luxuriante. Le lambroquin de type f m1 s’y trouve en parfaite cohérence : d’une part, sa symétrie bilatérale est à l’image de l’homme qui habite la case, d’autre part ses motifs sont, le plus souvent, issus de la stylisation de formes rencontrées dans la végétation tropicale environnante. Le lambroquin reste ainsi un objet familier, apaisant, rassurant. Sa seule audace réside dans le fait d’ tre une frise. En lançant un pont vers l’infini, vers l’ailleurs, vers une dimension supérieure, il rappelle discrètement que la case créole, plus généralement le milieu insulaire, est un monde clos et fini. Toute la fascination d’une île ne provient-elle pas de l’irrésistible envie d’en sortir ?

À l’heure actuelle, il ne reste plus que deux artisans fabriquant des lambroquins à La Réunion : M. Vee Nicko, à Cambuston, et M. Bailleux, à Étang-Salé-les-Hauts. Nous les avons rencontrés : tous deux paraissent désabusés.

Le lambroquin artisanal en bois, trop coûteux, est sur le point de disparaître au profit du lambroquin en tôle qu’une usine locale produit à la chaîne. Ces artisans parviennent à survivre en se consacrant principalement à la fabrication d’impostes, de balustres et de motifs décoratifs nouveaux qui n’ont plus rien de géométrique. Ni l’un ni l’autre ne forme d’apprenti : leur art va sans doute s’éteindre avec eux. L’industrialisation du lambroquin aboutira inévitablement à un appauvrissement des motifs, de moins en moins nombreux et de plus en plus standardisés. Il est dommage que l’art du lambroquin créole disparaisse alors qu’il est encore loin d’avoir exploré toutes ses potentialités géométriques : de jeunes artisans pourraient le renouveler grandement en dépassant le classique type f m1 pour exploiter pleinement les six autres types de frises que leur offrent les mathématiques.